Quelle cene del venerdì scandite da anonime pizze a domicilio tagliate senza senso. Quelle fette scambiate a lume di candela, romantiche ma divise in modo totalmente arbitrario. Quei triangolini solitari e asimmetrici mangiati freddi la mattina successiva.
Tutto questo, cari lettori di Dissapore in fissa eterna con la pizza, potrebbe essere a una svolta grazie alla geometria.
Due giovani matematici inglesi con la passione per la cucina, Joel Haddley e Stephen Worsley, hanno applicato complessi principi scientifici per spiegare al popolo mondiale dei pizzofili il modo corretto di tagliare la pizza.
E la fantasia vola!
Almeno 5 miliardi di pizze vengono vendute ogni anno nel mondo, le fette consumate ogni secondo sono 350, ma quante di queste sono uguali?
Immaginate che belle pizzate in compagnia senza faide per l’ultimo lembo superstite, senza corsa affannosa alla fetta più grande che lascia il malcapitato di turno con le briciole.
Per ora i nostri nuovi eroi hanno diviso la pizza in dodici fette, ma giurano di poter ripetere il taglio all’infinito attenendosi alla formula pubblicata nel loro lavoro dal titolo Infinite families of monohedral disk tilings.
Vediamo come funziona.
In principio i matematici hanno inventato un metodo per dividere la pizza in dodici parti identiche – sei fette partono dal centro verso l’esterno, altre sei dal cornicione verso l’interno.
S’inizia con tre tagli curvi che attraversano tutti i lati della pizza, poi ogni fetta viene divisa in due parti così da ottenere gruppi di fette esterni e interni.
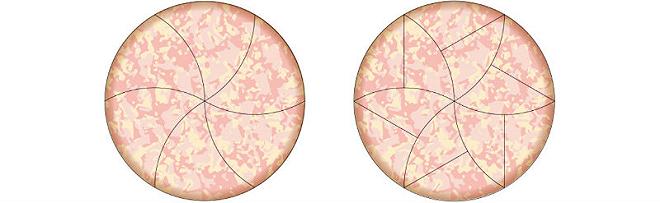
Se i tagli vengono fatti bene sembra un bel fiore simmetrico tra l’altro.
Dalla tecnica alla teoria matematica, il passo per i due giovani matematici è stato breve.
Ora sono in grado di affermare che è possibile formare tasselli in una pizza (identificata come una figura geometrica tonda) per un numero infinito di volte.
La regola da seguire è sempre la stessa: fare tagli in un numero dispari di lati, pentagoni o ettagoni, seguendo lo schema illustrato in precedenza (dall’interno verso l’esterno e viceversa, per poi dividere tutte le fette per due).
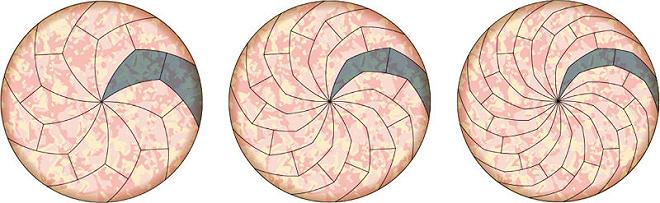
Haddley e Worsley sono andati oltre, modificando le forme, spuntando gli angoli e creando degli effetti visivi da psicofarmaci.
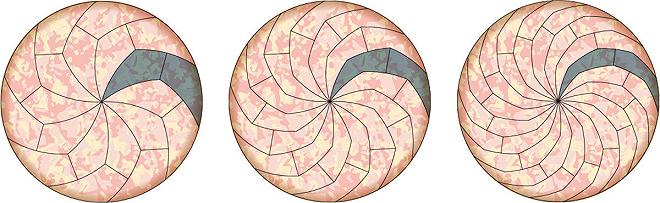
Dal punto di vista matematico si potrebbe continuare senza sosta.
Nella pratica di noi pizzomani impenitenti andare oltre il poligono a 9 lati potrebbe essere un problema.
Per ora il risultato pervenuto sul disco di pasta condito con pomodoro e aggiunte varie che chiamiamo pizza è questo.

Mandatelo a memoria, al prossimo ordine di pizza a domicilio saprete come impressionare gli amici .
[Crediti | Link: New Scientist]
